Формальные методы доказательства правильности программ и их спецификаций
Традиционные методы анализа ПО связаны с доказательством правильности программ (верификация программ). Начало этому направлению было положено работами П. Наура и Р. Флойда, в которых сформулирована идея приписывания точке программы так называемого индуктивного, или промежуточного утверждения и указана возможность доказательства частичной правильности программы (то есть соответствия друг другу ее предусловия и постусловия), построенного на установлении согласованности индуктивных утверждений.
Фундаментальный вклад в теорию верификации внес Ч. Хоор, высказавший идеи проведения доказательства частичной правильности программы в виде вывода в некоторой логической системе, а Э. Дейкстра ввел понятие слабейшего предусловия, позволяющее одновременно как соответствие друг другу предусловия и постусловия, так и завершимость. Методы доказательства правильности программ принесли определенную пользу программированию. Было отмечено, что эти методы указывают способ рассуждения о ходе выполнения программ, дают удобную систему комментирования программ и устанавливают взаимосвязи между конструкциями языков программирования и их семантикой. Если принять более широкое толкование термина "анализ программ", подразумевая доказательство разнообразных свойств программ или доказательство теорем о программах, то ценность методов анализа станет более ясной. В частности можно исследовать характер изменения выходных значений программы, количество операций при выполнении программы, наличие зацикливаний, незадействованных участков программы. Таким образом, в некоторых частных случаях методы верификации могут применяться и для доказуемого обнаружения программных дефектов.
Формальное доказательство в виде вывода в некоторой логической системе вполне надежно, но сами доказательства оказываются очень длинными и часто необозримыми. Рассмотрим следующий фрагмент программы.
integer r, dd; r:=a; dd:=d; while dd
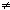d do dd:=2*dd; begin dd:=dd/2; if dd
Должно соблюдаться условие, что целые константы a и d удовлетворяют отношениям a
Рассмотрим последовательность значений, заданную выражениями для:
i=0 ddi=d i>0 ddi=2*ddi-1.
Далее с помощью обычных математических приемов можно вывести, что: ddn=d*2n (2.1.1)
Кроме того, поскольку d>0, можно сделать вывод, что для любого конечного значения r отношение ddr>r будет выполняться при некотором конечном значении k; первый цикл завершается при dd=d*2k. Решая уравнение di=2*di-1 относительно di-1, получаем di-1=di/2, что позволяет утверждать, что второй цикл тоже завершится. По окончании первого цикла dd=ddk и поэтому выполняется соотношение
0
Это соотношение сохраняется при выполнении повторяемого оператора второго заголовка. После завершения повторений (в соответствии с заголовком while dd
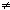
0
Далее мы доказываем, что после начала работы программы всегда выполняется отношение:
dd
Это следует, например, из того, что возможные значения dd имеют вид (см. (1)) d*2i при 0
k.Следующая задача состоит в том, чтобы показать, что после присваивания r начального значения всегда выполняется отношение
a
Оно выполняется после начальных присваиваний.
Повторяемый оператор первого заголовка (dd:=2*dd) сохраняет отношение (2.1.5), и поэтому весь первый цикл сохраняет отношение (2.1.5).
Повторяемый оператор из второго цикла состоит из двух операторов. Первый (dd:=2*dd) сохраняет инвариантность (2.1.5); второй тоже сохраняет отношение (2.1.5), так как он либо не изменяет значение r, либо уменьшает r на текущее dd, а эта операция в силу (2.1.4) также сохраняет справедливость отношения (2.1.5). Таким образом, весь повторяемый оператор второго цикла сохраняет отношение (2.1.5).
Объединяя отношения (2.1.3) и (2.1.5), получаем, что окончательное значение r удовлетворяет условиям 0
r(mod d), то есть r - наименьший неотрицательный остаток от деления a на d.И хотя методы доказательства правильности программ существенно ограничены для практического использования, тем не менее есть области, где данные методы могут найти прикладное значение.
При этом n и m связаны соотношением n=s*m, где s=log2r (в дальнейших рассуждениях log - логарифм по основанию 2). Наиболее целесообразно выбрать основание r=2? как наиболее экономное представление чисел в машине, ибо при r < 2? на представление чисел уходит больше памяти. Например, широко принятое на практике представление десятичных чисел в двоично-десятичном коде требует на 20 % большего объема памяти, чем двоичное представление тех же чисел.
Тем не менее, иногда полезно представлять ситуацию, когда r=10 или r=10k, например, при отладке программ.
Следует также обратить внимание на тот факт, что при выполнении арифметических операций над числами многократной точности, например, по классическим алгоритмам Кнута, основание r следует уменьшать, чтобы не возникло переполнение разрядной сетки. Так, для операции сложения уменьшение выполняется до r=2?-1, для умножения - до r=2?/2. Однако если архитектурой вычислительной системы предусмотрен флаг переноса или хранение промежуточного результата с двойной точностью, то можно возвращаться к основанию r=2?.
Алгоритм A*B modulo N - алгоритм выполнения операции модулярного умножения
Операнды многократной точности для данного алгоритма представляются в виде одномерного массива целых чисел. Для знака можно зарезервировать элемент с нулевым индексом. Особенности представления чисел при организации взаимодействия алгоритма с другими рабочими программами, при организации ввода-вывода и т.д. рассматриваются, например, в работе. В алгоритме использован известный вычислительный метод "разделяй и властвуй" и реализован способ вычисления "цифра-за-цифрой". Прямое умножение не следует делать по нескольким причинам: во-первых, произведение A*B требует в два раза больше памяти, чем при методе "цифра-за-цифрой"; во-вторых, умножение двух многоразрядных чисел труднее организовать, чем умножение числа многократной точности на число однократной точности. Так, в работе приводятся расчеты на супер-ЭВМ "CRAY-2" для 100-разрядных десятичных чисел: модулярное умножение методом "цифра-за-цифрой" выполняется примерно на 10% быстрее, чем прямое умножение и следующая за ним модульная редукция.
Алгоритм модулярного умножения (алгоритм P) приведен на рис.2.1, а на рис.2.2 представлен псевдокод процедуры ADDK.
Так как B[i]
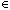P можно не вводить потому, что вероятность того, что B[i] будет равняться 0 пренебрежимо мала, если значение ? не достаточно малым. Ошибка затем все равно будет алгоритмом обнаружена. Проверка "if p_short-k*n_short>n_short DIV 2"
позволяет представлять k числом однократной точности и работать с наи-меньшими абсолютными остатками в каждой итерации. Значение операнда Pi на каждом шаге итерации должно быть ограничено величиной N.
Теорема 2.1. Пусть Pi - частичное произведение P в конце i-той итерации (т.е. в конце i-того цикла FOR алгоритма P). Тогда для любого i (i=[1,...,n]) abs(Pi)N, rm-1
rm.Доказательство теоремы 2.1. Доказательство теоремы проведем методом индукции. Если k=abs(p_short) DIV n_short, где DIV - целочисленное деление, то
p_short=(k+?)*n_short, (2.1.6)
где k - целое, 0
? < 1.Проверка "if p_short-k*n_short>n_short DIV 2" есть ни что иное, как проверка
? > 0.5 (2.1.7)
На i-том шаге алгоритм вычисляет:
P'=Pi-1*r+A*B[i] (2.1.8)
Возможны два варианта:
Вариант 1. Если k=0, т.е. n_short>abs(p_short) (см. алгоритм), то суммирование при помощи процедуры ADDK не производится и утверждение теоремы выполняется, т.е. abs(Pi) < N .
Вариант 2. Если k > 0, т.е.
n_short < abs(p_short) (2.1.9)
Здесь также возможны два варианта:
Вариант A:
p_short < 0 (2.1.10)
Из (2.1.9) и (2.1.10) следует P' и так как Pi=-P'+k*N (см. алгоритм), то согласно (2.1.7)
Pi= ?*N, если ?
и так как Pi=-P'+(k+1)*N, то
Pi=-(1-?)*N, если ? > 0.5 (2.1.12)
Алгоритм P
m_shifts:=0; while n[m_shifts]=0 do begin shift_left(N and A); m_shifts:=m_shifts+1; end; m:=m_shifts; reset(P); n_short:=N[m]; for i:=n downto 1 do begin shift_left(P);
{сдвиг на 1 элемент влево или
умножение P*r} if b<>0 then addk(A*B[i],{to}P); let p_short represent the 2 high
assimilated digits of P; k:=abs(p_short) div n_short; if p_short-k*n_short > n_short div 2 then
k:=k+1; if k> 0 then begin if p_short < 0 then addk(k*N,{to} P) else addk(-k*N,{to} P); end; end;{for} right shift P, N by m_shifts; if P < 0 then P:=P+N; write(P); {P - результат}
Рис. 2.1. Псевдокод алгоритма модулярного умножения A*B modulo N
Алгоритм ADDK
carry:=0; for i:=1 to m do begin t:=P[i]+k*N[i]+carry; P[i]:=t mod r; carry:=t div r; end; P[m+1]:=carry; write(P); {P - результат}
Рис.2.2. Псевдокод алгоритма вычисления P+k*N (процедура ADDK)
Вариант B:
p_short>0 (2.1.13)
Из (2.1.9) и (2.1.13) следует P'>N и так как Pi=P'-k*N, то согласно (2.1.7)
Pi=-? *N, если ?
и так как Pi=P'-(k+1)*N, то
Pi=(1-?)*N, если ? > 0.5 (2.1.15)
Во всех случаях (2.1.11), (2.1.12), (2.1.14) и (2.1.15), так как 0
.
Примечание. Для чего нужна проверка (2.1.7)
"if p_short-k*n_short>n_short DIV 2" ?
Пусть в конце каждой итерации P принимает максимально возможное значение Pi-1=N-1, а N, A и B[i] заведомо тоже велики: N=rn+1-1, A=rn+1-2, B[i]=r-1. Тогда на i-том шаге согласно (2.1.8):
Pi'=(rn+1-2)*r+(rn+1-2)*(r-1)=2*rn+2-rn+1-4*r+2(2.1.16)
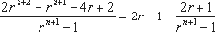
При достаточно большом m, если не введена проверка (2.1.6), то k < 2*r-1, по условию же 0< k < r -1. И из (2.1.16) и (2.1.17) видно, что P придется представлять m+2 разрядами (что определяется слагаемым 2*rn+2), по условию же m+1. Если же ввести проверку (2.1.7), то даже при ?=0,5 т.е.
Pi-1=(N-1)/2 и с учетом того, что если неравенство (2.1.7) выполняется, то Pi меняет знак на противоположный (сравн. (2.1.11), (2.1.12), (2.1.14) и (2.1.15)), из (2.1.6) и (2.1.7) получим, что 0
В алгоритме P используется также известный метод, когда для получения частного от деления двух многоразрядных чисел, используются только старшие цифры этих чисел (см., например, алгоритм D в работе ).Чем больше основание системы счисления r, тем ниже вероятность того, что пробное частное k от деления первых цифр больших чисел не будет соответствовать действительному частному.
Методы доказательства правильности программ могут быть применены для анализа безопасности ПО при существенных ограничениях на размеры и сложность создаваемых программ. Поэтому в частных случаях они могут оказаться более эффективными, чем другие известные методы анализа программ, которые исследуются в следующих разделах данной работы.
